本文撰写时间为2023/01/19 参考wicast C的文章（链接：https://wicast.medium.com/-531cd9ed9ea）在此基础上使用macdeployqt进行打包

不使用brew 安装qt6

brew 安装的qt6 在使用macdeployqt会有类似如下错误导致，qv2ray无法正常打包framework

ERROR: Cannot resolve rpath "@rpath/QtGui.framework/Versions/A/QtGui"
ERROR:  using QList("/Users/wany/Qv2ray/build3/lib")
ERROR: Cannot resolve rpath "@rpath/QtCore.framework/Versions/A/QtCore"
ERROR:  using QList("/Users/wany/Qv2ray/build3/lib")
ERROR: Cannot resolve rpath "@rpath/QtWidgets.framework/Versions/A/QtWidgets"
ERROR:  using QList("/Users/wany/Qv2ray/build3/lib")
ERROR: Cannot resolve rpath "@rpath/QtGui.framework/Versions/A/QtGui"
ERROR:  using QList("/Users/wany/Qv2ray/build3/lib")
ERROR: Cannot resolve rpath "@rpath/QtCore.framework/Versions/A/QtCore"
ERROR:  using QList("/Users/wany/Qv2ray/build3/lib")

卸载qt6

brew remove qt@6

使用qt.io官方安装器安装

https://www.qt.io/download-qt-installer

可能需要注册账号

参考：https://blog.csdn.net/ilovejujube/article/details/128035916

安装依赖

brew install go grpc cmake v2ray openssl

编译 Qv2ray

编译

注意替换CMAKE_PREFIX_PATH为自己的Qt路径

git clone https://github.com/Qv2ray/Qv2ray -b dev
cd Qv2ray
mkdir build
cd build
cmake -DQV2RAY_QT6=ON -DQV2RAY_USE_V5_CORE=OFF -DCMAKE_BUILD_TYPE=Release -DQV2RAY_AUTO_DEPLOY=ON -DCMAKE_PREFIX_PATH=/Users/wany/Qt/6.4.2/macos -DOPENSSL_ROOT_DIR=/opt/homebrew/Cellar/openssl@3/3.0.7 ..
make -j16

运行

open qv2ray.app

编译 QvPlugin-Trojan-Go

注意替换CMAKE_PREFIX_PATH为自己的Qt路径

git clone https://github.com/Qv2ray/QvPlugin-Trojan-Go -b dev
cd QvPlugin-Trojan-Go
mkdir build
cd build
# 要让插件用 QT6
cmake -DQVPLUGIN_USE_QT6=ON -DCMAKE_PREFIX_PATH=/Users/wany/Qt/6.4.2/macos -DCMAKE_BUILD_TYPE=Release ..
make -j16

三明治攻击案例分析

抢跑阶段

1. Mev bot在uniswap-v2上卖出ETH买入NCR。
2. 再将买入的NCR在uniswap-v3上卖出，买入USDC。引起USDC在uniswap-v3的NCR-USDC LP池中升值抬高了接下来受害者交易的成本。（其他池不受影响）

https://etherscan.io/tx/0xc6d53c38434effa63fdf3b763759b1fa9699219af99c9e5efca53a8bbb44804a

受害者行为

受害者在uniswap-v3用较高的成本上卖出大量NCR，买入USDC。

https://etherscan.io/tx/0x88d125526b4a1549108a508663104c643160a349876a576be64a3109dc082576

尾随阶段

1. Mev bot在uniswap-v3上卖出USDC买入NCR成功换出更多的NCR。
2. 再将换出的NCR在uniswap-v2上卖出，换回WETH。

https://etherscan.io/tx/0x0f66853c690105c5f3a080ce75d75a04a35bd4eb8618f7878ee7e0e3dd53ab82

利益分析

用户损失\Mev Bot毛利润：0.099336744926763451 ether（$303.53）

Mev Bot净利润（去除矿工费）：0.001781203268032581 ether（$5.44）

矿工净利润（去除basefee）：0.08727896012374656 ether（$266.69）

燃烧费用：0.00978678484422912 ether（$29.9）

在此利益分配中，矿工通过套利交易手续费获取套利总额的97.46%

uniswap公式

最后把$\theta=1-\rho$（对于uniswap是0.3%）代入公式:

$$\Delta{y}=(997·\Delta{x}·y)/(997·\Delta{x}+1000x)$$

公式符合UniswapV2Library的getAmountOut函数。

Flashbots Auction

Flashbots Auction提供私人交易池 + 密封投标区块空间拍卖机制，允许区块生产者无需信任地外包寻找最佳区块构建的工作。
在常规的以太坊交易池中，用户将交易广播到公共点对点网络并指定一个燃料价格，该价格表明他们愿意为以太坊链上的每个计算单元支付多少。矿工收到这些交易，按gas价格排序，并使用贪心算法生成一个区块，试图通过交易费用获得最大价值。
以下是该机制的关键问题：

• 用户为了抢占套利机会，纷纷通过提高gas price，以便抢占第一个套利机会（只有第一笔套利能够成功），在短时间内使gas price巨幅提升，影响网络稳定。
• 只有一笔套利交易可以成功，其他的交易均失败，消耗区块链空间。
• 恶意用户为了抢占套利机会，这导致了诸如垃圾邮件之类的替代策略来增加获胜的可能性，从而进一步增加无谓损失。
  相反，Flashbots Auction基础设施使用第一价格密封投标拍卖，允许用户私下交流他们的投标和细化交易订单偏好，而无需为失败的投标付费。这种机制最大限度地提高了矿工的收益，同时为给定 MEV机会价值的价格发现提供了一个有效的场所。至关重要的是，这种机制消除了抢先漏洞。

技术架构

Flashbots Auction引入了一种新的eth_sendBundleRPC请求，它标准化了通信通道中的消息格式。此消息称为“Flashbots Bundle”。目的是将多笔交易顺序捆绑，竞拍后交由矿工出块。

{
  "jsonrpc": "2.0",
  "id": 1,
  "method": "eth_sendBundle",
  "params": [
    {
      txs,               // Array[String], A list of signed transactions to execute in an atomic bundle
      blockNumber,       // String, a hex encoded block number for which this bundle is valid on
      minTimestamp,      // (Optional) Number, the minimum timestamp for which this bundle is valid, in seconds since the unix epoch
      maxTimestamp,      // (Optional) Number, the maximum timestamp for which this bundle is valid, in seconds since the unix epoch
      revertingTxHashes, // (Optional) Array[String], A list of tx hashes that are allowed to revert
    }
  ]
}

搬砖套利

因为DEX各池子的价差，Mev Bot分析后在DEX之间搬砖套利。

案例具体过程

1. Mev Bot在sushiswap卖出7.38WETH，买入2698.66 RUNE。
2. 随后再将买入的2698.66 RUNE在uniswap-v3卖出换成7.70个WETH完成套利。

https://etherscan.io/tx/0xa8930ae6a17a679ea5abd4b7274dc27416be5d62379c848ade8779e876986f7b

利益分析

Mev Bot毛利润：0.329689032623411672 ether（$1021.11）

Mev Bot净利润：0.314207274249977546 ether（$973.16）

矿工利润：0.011232792714802698 ether（$34.79）

简单的搬砖套利程序

Flashbot提供一个简单的套利工具，用于从两个DEX中相同的LP池套利。
https://github.com/flashbots/simple-arbitrage

具体流程

1. 获取两个DEX所有LP池的reserves数据。
2. 计算两个DEX相同的LP池reserves的可套利空间。
3. 构造交易调用链上部署好的FlashBotsMultiCall合约。
4. 将交易构建完成，模拟交易，如果成功则构建simulate。
5. 将simulate发送给flashbots。

项目不足的地方

计算最佳收益使用二分搜索的方式，时间复杂度高，并且代码不完善、不精确。

改进

理论上交叉套利是存在一个最值的，我们可以通过uniswap的公式统一成一个交叉套利的公式，求出最值。此公式论文：https://arxiv.org/pdf/1911.03380.pdf
github上也有大神通过此论文改进了getBestCrossdMarket函数：https://github.com/jacksonConrad/better-simple-arbitrage

输出结果

参考文献

https://www.cxyzjd.com/article/sanqima/109667469
https://arxiv.org/pdf/1911.03380.pdf
https://docs.flashbots.net/flashbots-auction/overview

Starkware

StarkWare是一个为了解决区块链的可扩展性和隐私的组织。 StarkWare开发了一个完整的解决方案，使用透明零知识证明（zk-STARK）技术，zk-Rollup和Validium模式组成Volition来生成和验证计算完整性的证明。StarkWare的密码证明可以做到零知识、简洁、透明和后量子安全的特点。 StarkWare所研发的产品主要有：StarkNet、StarkEx、Cairo。

扩展解决方案

StarkEx

StarkEx是基于有效性证明的以太坊可扩展性解决方案。 它可以在zk-Rollup或Validium数据可用性模式下运行。
基于StarkEx之上架构使用Cairo编写的应用程序（dydx、Imutable X…）都会定义自己的业务运行逻辑，并在StarkEx服务上运行。 该系统具有链上组件和链下组件。 链下组件持有状态，命令执行系统中的交易，并将状态更新发送到链上组件。 链上组件持有状态承诺，持有系统资产，并负责执行状态转换的有效性。

系统元件

StarkEx系统包含以下组件：

• 应用程序：接收用户交易的链下组件，定义业务运行逻辑和执行的顺序。最终，它将交易发送到StarkEx服务。
• StarkEx服务：链下组件，负责批处理一组操作，根据这些操作更新系统状态。针对每一批，StarkEx服务将发送此批的操作(作为Cairo执行痕迹)到SHARP进行有效性证明，一旦证明被验证，它将新状态发布在链上。 状态由Merkle tree呈现，其叶子是保险库。每个保险库的结构和内容根据所实施的特定业务逻辑而有所不同。Merkle tree root代表要在链上提交的状态承诺。
• SHARP(Prover)：Cairo程序的共享证明服务。 它接收来自不同应用程序的证明请求，并输出证明以证明Cairo程序执行的有效性。输出的证明可以在多个证明请求之间共享。
• STARK验证器(Verifier)：这是一个链上组件，用于接收状态更新有效性证明并验证该证明是否有效。
• StarkEx合约：该合约有两个主要功能。 第一个是在确认有效性条件得以满足后更新系统状态。第二个功能是以自主托管方式管理在StarkEx中的进出资金，这意味着在任何情况下，用户都可以提取其资金。

系统中的所有交易都通过应用程序执行，并将撮合好的交易发送到StarkEx服务。 StarkEx服务对交易进行批处理更新状态，并将批处理后将SHARP需要的参数发送到SHARP（共享证明服务）生成一份证明来表明批处理的有效性。SHARP将STARK证明发送给STARK验证器进行验证。服务随后发送一份链上状态更新交易到StarkEx合约，仅在证明被验证器验证有效时，交易才会被接受。

用户以两种方式与系统交互：

• 通过发送链上交易到StarkEx合约。
  ‌‌当用户想要使用该系统时，他们首先将StarkKey注册到StarkEx合约中的以太坊地址。StarkKey用于验证用户的链下交易。 然后，用户将其资金存入StarkEx合约。 在应用程序接受存款后，用户可以在链下使用其资金。
• 发送链下交易到应用程序。
  用户将由StarkKey签名的转账或限价单直接提交给应用程序。限价单经由链下程序定序匹配，并作为结算发送给StarkEx服务。转账行为照原样发送。不同类型的转账交易可以由额外的逻辑来执行。
  ‌为提取资金，用户应向应用程序提交链下提款请求。此请求被发送到StarkEx服务，一旦包含提款的状态更新被接受，用户就可以在链上获取其资金。

‌为了防止审查，如果用户的提款请求没有得到实现，他们可以使用强制操作来强制执行。

Immutable X

Immutable X使用Starkware基于StarkEx提供的方案。具体架构与上文大同小异，不再赘述。

以太坊上NFT接入

NFT接入，本质上需要让以太坊上的IMX合约拥有NFT的铸造权。

新的NFT接入

对于要新建的NFT只需要在自己的ERC721合约的基础上实现IMX给定的Mintable接口。

pragma solidity ^0.8.4;

import "@openzeppelin/contracts/token/ERC721/ERC721.sol";
import "./Mintable.sol";

contract Asset is ERC721, Mintable {
    constructor(
        address _owner,
        string memory _name,
        string memory _symbol,
        address _IMX
    ) ERC721(_name, _symbol) Mintable(_owner, _IMX) {}

    function _mintFor(
        address user,
        uint256 id,
        bytes memory
    ) internal override {
        _safeMint(user, id);
    }
}

已部署的NFT接入

对于已部署过的合约，需要写一个新的合约包装进旧的合约。
确保此合约可以铸造NFT，并且只有IMX可以调此合约的mintFor方法。

import "@imtbl/IMX-contracts/contracts/Mintable.sol";
import "@openzeppelin/contracts/access/Ownable.sol";

contract YourContract is IMintable, Ownable {

    function mintFor(
        address to,
        uint256 quantity,
        bytes calldata mintingBlob
    ) external override {
        // TODO: make sure only Immutable X can call this function
        // TODO: mint the token!
    }

}

创建项目 (project registration)

一个项目相当于一个超级管理员，并且和一个owner地址（拥有铸造权限）关联。用户可以在项目中发行多个合集（collections），IMX规定每个项目可以创建的collection数量有限制（一个月五个合集）。创建完项目后会生成对应的projectId。

 const params: CreateProjectParams = {
  name: '项目名字',
  company_name: '公司名字',
  contact_email: '联系邮箱',
};

let project;
try {
  project = await user.createProject(params);
} catch (error) {
  throw new Error(JSON.stringify(error, null, 2));
}

合集注册 (collection registration)

合集（collection）代表一个已经在以太坊网络上部署好的ERC721合约。为了能在IMX网络上铸造资产，首先需要在IMX上注册这个合集。
合集注册也是通过IMX提供的sdk或api完成，参考代码如下：

  const params: CreateCollectionParams = {
  name: '合集的名字',
  // description: 'ENTER_COLLECTION_DESCRIPTION (OPTIONAL)',
  contract_address: collectionContractAddress,
  owner_public_key: ownerPublicKey,
  // icon_url: '',
  // metadata_api_url: '', //<metadata_api_url>/<token_id>
  // collection_image_url: '',
  project_id: parseInt(projectId, 10),
};

let collection;
try {
  collection = await user.createCollection(params);
} catch (error) {
  throw new Error(JSON.stringify(error, null, 2));
}

在IMX上注册一个合集的例子可以参考这里。

元数据注册 (metadata schema registration)

IMX允许项目为他们的资产指定元数据属性，这些元数据属性可以更好的帮助交易市场（marketplace）执行复杂的过滤查询，这样帮助用户更精准的发现他们想要的资产。更多资产元数据的例子可以参考这里。
元数据注册也是通过IMX提供的sdk完成，参考代码如下：

const params: AddMetadataSchemaToCollectionParams = {
    metadata: [
      {
        name: 'EXAMPLE_BOOLEAN',
        type: MetadataTypes.Boolean,
        filterable: true,
      },
      // ..add rest of schema here
    ],
  };

  const collection = await user.addMetadataSchemaToCollection(
    collectionContractAddress,
    params,
  );

  log.info(
    component,
    'Added metadata schema to collection',
    collectionContractAddress,
  );
  console.log(JSON.stringify(collection, null, 2));

在IMX上创建注册元数据的例子可以参考这里。

功能时序图

铸造

管理员给IMX Engine发送铸币请求并附带签名，IMX Engine执行批次化后交由Prover进行生成有效性证明生成Proof提交到以太坊的验证合约进行验证。

存款

用户发送代币转账到以太坊合约中，IMX Engine监听到存款事件后更改网络状态后交由Prover进行生成有效性证明生成Proof提交到以太坊的验证合约进行验证。

取款

• 一般情况：链下触发。用户发起提款请求。IMX Engine执行批次化后交由Prover进行生成有效性证明生成Proof提交到以太坊的验证合约进行验证。验证通过后用户在以太坊上调用取款取出资产。
  
• 特殊情况（例如：IMX Engine down掉）用户可以直接调用链上的紧急退出功能经过锁定时间窗口后取出所有资产。

交易

IMX Engine内维护了一个中央订单簿。用户创建卖单将在IMX Engine中进行维护。当IMX Engine接收到对应买单会自动撮合，随后交由Prover进行生成有效性证明生成Proof提交到以太坊的验证合约进行验证。

SDK && API

Immutable X SDK 是一个由Immutable创建的Javascript包，允许与Immutable X的API进行简单接口。主要使用的包是 Link SDK和Immutable X Client。
Immutable X Client用于大多数后端操作，Link SDK用于前端、面向用户的交互。

SDK
API
API调用限制

探索 StarkNet

几个概念

状态机

Y(S, T)= S'

给定一个旧的有效状态 （S）和一组新的有效交易 （T），以太坊状态转换函数 Y（S，T） 产生新的有效输出状态S'。

Re-Execution

是一种通过执行相同的计算来证明一个事实。

零知识证明

零知识证明的目标是让验证者相信证明者拥有某个秘密(withness)，满足某种关系，而无需向验证者或其他任何人透露秘密本身。
定义：

• 完整性（Completeness）：如果证明者是诚实的，那么她最终会说服验证者。
• 可靠性（Soundness）：证明者只能说服验证者该陈述是否属实。
• 零知识性（Zero-knowledgeness）：除了知道陈述是真实的，验证者不知道任何额外的信息。

区块链解决了什么问题？

信任问题：系统A如何相信系统B陈述了一个事实。

经典系统

• 传统中心化账本系统：数据都存在一个大型计算机的账本系统中，用户使用时必须相信这个系统。
• 经典区块链系统：区块链具有包容性和问责制。每个操作员都有一个账本系统，操作员除经过自己验证数据可信之外，并不相信任何人的数据。每个操作员都需要验证所有交易的有效性。

区块链系统为了验证数据，所有交易都要公开在网络中，牺牲了数据的隐私性。

解决方案

• 增量扩容：通过扩大区块内交易数量或计算逻辑会导致操作节点需要更强的性能来处理更多的数据，越来越多的节点因为机器性能不足从而退出网络。导致节点数量减少，偏向于中心化。
  
• 有效性证明系统：有效性证明将操作员拆分为二：证明者（Prover）和验证者（Verifier）。证明者执行数据逻辑生成一个证明（Proof）交由给验证者网络，使验证者可以通过验证这个证明本身就可以相信证明者数据的有效性。有效性证明是个NP问题（证明困难，验证简单）。既保证了数据的隐私，又可以让验证者轻易的相信数据可靠。
  

ZK-STARK Proofs

zk-STARK不需要可信设置（non-setup），是一种透明化的零知识证明系统。



验证者只需验证Proof就可以相信证明者发送的最新状态，而不需要验证交易本身。

Zkp常见系统比较

从上图可看出：STARKs的证明、验证和见证大小复杂度均高于其他系统（多项式对数复杂度随着规模扩大，系统效率越高，所以要进行批次化）。优点是不需要可信设置（Trusted setup），并且他的加密假设是基于哈希碰撞，具有良好的后量子安全的特点。

Cairo Language

Cairo是一种用于为一般计算创建STARK证明程序的图灵完备语言。Cairo为StarkEx提供支持，后者可扩展Mainnet上的应用程序（包括 dYdX、Sorare、Immutable X和 DeversiFi）。Cairo是StarkNet的原生智能合约语言。

StarkNet

StarkNet是无须许可的去中心化的zk-Rollup。它作为以太坊的Layer2网络运行。在StarkNet上使用Cairo开发的dApp，可以支持无限规模的计算。
特点：

• 可扩展性和完整性：StarkNet支持规模化，可以使用Layer1以太坊的安全性，通过在链下生成STARK证明，然后在链上进行验证。
• 通用性：在StarkNet上，开发人员可以使用Cairo编写智能合约轻松部署任何业务逻辑。
• 可组合性：StarkNet提供以太坊级别的可组合性，促进轻松开发和创新。

路线图

• 阶段一 Planets: 单应用、单操作节点的Rollups
• 阶段二 Constellations: 多应用、单操作节点的Rollups
• 阶段三 Universe: 多应用、去中心化节点的Rollups

当前进度

架构图

StarkNet Full Node：StarkNet网络中的一个节点，仅用于查询当前StarkNet状态。
StarkNet Sequencer Node：StarkNet网络中用于定序和生成零知识证明的节点。相当于StarkNet的矿工。

递归零知识证明

定义

递归零知识证明：使用前一个状态的Proof以及当前交易作为输入，接下来Prover去尝试证明前一个状态的Proof以及当前交易是否有效，如果全部验证通过，程序会输出一个新的状态及一个Proof，过程如下图所示：

递归零知识证明验证：只要验证前一个状态的Proof就可以验证整个链的状态，比如：当验证Proof #5状态是正确的，相当于递归验证了Proof #4，Proof #3。

Mina（旧称Coda）项目，将整个区块链维持在22k，其中就使用了递归零知识证明。
优点：递归零知识证明有非常好的聚合（压缩）、节省空间的优点。

多层网络

某些dApp需要特殊的定制，这可能更好地在此层基础上，构建一个新的独立层提供服务。
具体过程：

• 每层网络都有一个Cairo程序，它可以作为该层网络的共识，或具体的业务。
• 下层网络提交Proof和State Update（在zk-rollup需要包含与之相关的Merkle Tree，在Validium下只需要Merkle Tree Root）到该层Prover进行定序和批次化。
• Prover使用State Update更新该层网络状态对应下层网络Key「保险库」的State。
• Prover调用该层Cairo程序并输入Inputs（更新前的网络状态）、Outputs（更新后的网络状态）、txs（下层网络提交的Proofs和State Update），生成该层的Proof和State Update，并将提交到上层网络的Verifer验证。

注意：此处是一个递归化的过程。
每层网络中都维护一个网络状态。
利用零知识隐私化的特性，每层网络只需要关心当前层的网络状态合理化而无须关心下层网络本身。

经典Layer2架构

• L2 Contract：记录Layer2 State/Root的合约。
• Verifier Contract：用于验证Layer2状态转移有效性的Verifier的合约。
• 桥接Layer1、Layer2的资产出入管理合约。
• ERC20/ERC721账户模型对应网络的镜像。

应用在Layer3上

与Layer2在Layer1一样，Layer3也可以使用相同的结构并添加差异化的功能。

参考资料

https://medium.com/starkware/fractal-scaling-from-l2-to-l3-7fe238ecfb4f
https://medium.com/starkware/redefining-scalability-5aa11ffc5880
https://iosgvc.medium.com/scaling-summit-2021-keynote-recap-stark-validity-rollup-an-ultimate-scaling-technology-9cc62b307f69

什么是MEV

MEV是矿工可提取价值（Miner Extractable Value）的缩写。由于区块链并没有要求矿工对交易打包顺序做出强制要求，矿工是可以自主选择对内存池中的待处理交易进行重新排序，由此矿工从用户那里获得了额外的利润，这部分利润价值就被称为MEV。

DeFi的兴起。MEV价值呈指数增长。

浏览器链接：https://explore.flashbots.net/

存在的角色

矿工

矿工是工作量证明机制的核心。矿工的工作任务是将用户发来的交易进行打包，并通过工作量证明提交到区块链上。

矿工可以在不影响交易原子正确的前提下对多笔交易进行排序、包含、剔除等操作。

通常来说，矿工为了寻求利润最大化会将待打包的交易交易按照gas price进行排序。然后将最前面的N笔交易进行打包入块。

当然出于某些场景需求，矿工也可以按照他们想要的交易顺序进行打包。比如矿池定制化交易加速功能、对异常地址进行风险控制等等。例如：
比特大陆交易加速服务

套利机器人

虽然现在常用的说法是“矿工可提取价值”，但实际上大多数MEV行为是由第三方机器人，而非矿工，发起的。这些机器人通过提高支付给矿工的交易费来操纵区块中的交易排序。这意味着就算矿工仅按照gas price高低排序交易，也会出现MEV问题。然而，MEV还可以被视作是矿工可以提取的最大价值上限，因为矿工是最终决定区块中交易顺序的一方。

如何套利

有利的套利

如果套利发生在「世界状态」发生之后，套利机器人对市场变化作出的合理的反馈。那么这种套利即是合理的套利。

搬砖套利

用户在交易平台进行了一笔大额交易导致价格下滑，产生了较大的套利空间。套利机器人进行套利交易，将市场价格套利至真实价格水平。此类型的提取MEV大多是发生在链上事务发生后，套利机器人对市场进行反应，不会损害原始交易者的利益。
txid:0xb72689042f313adbffbe4d192b0febc4c8a8346b75a549d5b4d4795b37180488

清算机器人套利

有些协议的运转需要依赖于MEV，比如对Aave Protocol、MakerDAO、Compound的清算。在DeFi抵押借贷协议中，当抵押物价值下降时，如果没有补足或者出售抵押资产，就会触发清算程序。清算人可以以低于市场价格3%-5%的折扣，获得如ETH这样的抵押资产，而这3%-5%的折扣价值，就是MEV。

有害的套利

如果套利发生在「世界状态」改变之前，即机器人有预知「世界状态」改变的能力，那么这种操作会危害于区块链上的正常参与者。

三明治攻击

试想下，如果我们有能力在大资金买卖交易前后各插入一笔交易（买在低点，卖在高点）岂不是是一个稳赚不赔的策略？

如图所示，套利机器人过程主要分以下4个阶段。

• 阶段一：用户创建大额买单交易并进行广播，此时交易在内存池中未打包入块。
• 阶段二：套利机器人从交易内存池中捕获到用户交易，计算交易可套利价值空间，构造两笔交易进行广播。一笔以高于用户gas price创建买单进行广播，另一笔以低于用户gas price创建一笔卖单。
• 阶段三：交易机器人买单先成交，随后用户交易成功打包入块，价格拉升。
• 阶段四：价格拉升后，交易机器人卖单成功打包入块，完成套利。

矿工与套利机器人的收益来源是用户损失的部分。

MEV对网络的危害

• 拉高手续费：当DeFi各类资产价格发生波动，可套利的机会与利润空间也越来越多。机器人纷纷抬高gas price来争抢这笔利润，短时间使手续费价格巨增。

• 增加无效交易数量：MEV最终只会有一笔交易可以成功套利，其他的都会以失败告终。这些无效的交易也会像垃圾一样占用区块链的空间。

• 损害用户利益：套利机器人为了争抢套利机会，往往会抬高交易费，支付的交易费往往占套利所得收益的很大比例，而这些交易费最终直接落入了矿工的口袋。也就是说，虽然矿工没有亲自开展套利交易，但仍是这类MEV行为的最大受益者。

• 区块链频繁重组风险：对于矿工来说，如果MEV的价值远大于重组区块带来的损失。那么众多矿工都会尝试对不利于自己的区块进行重组。这导致的后果包括：交易确认时间变长，用户在平台的体验下降；增加了51%算力攻击的可能性。

MEV本质上是个零和游戏，损失的是链上用户，受益的是矿工和套利者。

缓解MEV重组风险

• 额外的安全性激励：除了区块奖励之外(如EIP-1559提议销毁的BaseFee，或状态租金)，稳定的矿工收入来源是对协议安全的补充，并可以帮助缓解MEV问题。
• 最终确定性 (Finality)：工作量证明 (PoW) 只有概率上的最终确定性。而基于拜占庭容错的算法（BFT）更能保证最终确定性，并且仅仅重组单个被敲定的区块就需要程度更深的合谋，该算法使得时间盗贼攻击更加困难。然而，如果MEV的激励足够高，那么即使合谋的难度较高也值得尝试了。再者，参与者对于其提议的区块，仍然有权任意排序交易，因此仅凭最终确定性无法解决“一般”的抢跑交易问题。
• 权益证明 (Proof-of-Stake)：基于新一代PoS的区块链（Casper FFG、Tendermint）中，尝试重组的验证者会遭受罚没惩罚，因此使得时间盗贼攻击成本更高，尤其是与最终确定性结合时。然而，只要MEV的激励足够高，即使在罚没惩罚的警示下也可能会捕获MEV。

以上方案在一定程度上缓解了矿工为了利益频繁重组区块带来的风险，但是对于套利机器人并无作用。

项目与服务

• Flashbots：是一家旨在降低由矿工可提取价值 (MEV) 对智能合约公链构成负外部性影响和存在风险的研发机构，该机构希望为智能合约公链打造一个无需许可、透明、公平的生态系统。（mev-geth和mev-relay）。他们的密封投标拍卖模型允许任何人通过贿赂提交交易，从而减轻以太坊网络的压力并减少矿工为最大化MEV所需的串通数量。对于同一笔套利只有一笔交易能够通过mev-relay下发给矿工，从而缓解了网络的拥堵以及手续费的水涨船高。但是并没有解决普通用户的三明治攻击问题。
  
• Taichi Network：由目前以太坊算力第二大矿池星火矿池创立，用户可以通过太极网络提供的接口直接发送交易到星火矿池的隐私池。由于星火矿池并不对这笔交易进行网络公开发布，这笔被发送出去的交易在未被正式确认前，在Etherscan上无法看到该笔交易的状态。
• bloXroute：提供隐私通信功能，允许交易在不被暴露的情况下直接到达矿工手中。bloXroute的BDN（区块链分发网络）通过自己的网关软件将区块链节点与BDN链接，网关软件和区块链节点首先翻译从区块链进入BDN的信息。然后，在第二层，它会进行区块压缩。通过极大缩小区块大小，使其随后更高效地在区块链分发网络（BDN）中发送/传输。

以上方案都在一定程度上解决了套利机器窥视内存池交易所带来的「抢跑」，但无法解决矿工本身套利的问题。

如何使用技术手段来避免MEV

思路是：交易可以在memory pool存储池中加密，并在排序完成后解密。这样任何人在交易定序前都不知道交易的内部细节。

可信式硬件（Trusted Hardware）

SGX代表Software Guard eXtensions，这是一个提供硬件内存加密的指令集，其中特定的代码和数据被隔离在「飞地」中，它们可以在不暴露于外部代码的情况下运行。

它以如下流程运行:

• 每个矿工都有一个SGX，他们有一个协议，用于共享只有在SGX中才能访问的加密密钥。
• 所有p2p内的交易都需要通过SGX内给定的公钥进行加密。
• SGX内部可以解密并验证交易的合法性，并构造一个pending block，并将block hash发送给外部用于PoW计算。
• 外部计算出PoW值后提交给SGX，SGX验证合法后将完整区块返还给外部进行广播。

优点：可以不用修改现有协议，SGX可以作为一个选项，添加到现有协议中。
缺点：虽然解决了交易内存池的可见性，抵挡了外部机器人对memory pool的窥视，但是对于矿工来说。如果MEV的价值远远大于报块可获得的奖励，矿工将在解密交易后重新rehash（非确定性共识下，例如PoW)。并且SGX依赖intel的指令集，并不能保证绝度安全。如果当利益足够大的情况下，某人通过SGX的漏洞找到私钥这个系统就不能运行了。

基于时间锁加密（TimeLock Encryption）

代表：STARKware’s Veedo
将交易进行加密后到内存池中，由矿工将加密后的交易打包到区块链上（事务为执行），同时将私钥通过例如VDF（可验证延迟函数)等方式，交由矿工进行延迟解密。N个块后矿工成功解密，将解密后的交易和Proof提交到区块链上进行验证，此时事务将真正执行。

• 所有的交易都需要加密，任何人都可以在X个计算周期后完成解密。
• 矿工将在加密交易上链后N区块开始解密，并在N+X区块后完成解密并提交到区块链上。
• 矿工必须在N+Y（Y>X）个区块之前完成解密交易的上链，否则交易将失效。

流程如下：

• 用户将经过同态隐藏的信息（可能是hash）交给矿工进行打包。
  

• 矿工成功将数据写入区块。
  

• 矿工对VDF进行解密（VDF保证在N个块之后才能解开），同时产生新的区块。
  

• N个块后，矿工解开交易生成解密后的交易和一个Proof，合约验证Proof的合法性再将解密后的数据写入区块链。
  

缺点： 所有的交易都得过这套系统，不能作为一个选项。并且交易有延迟对用户体验不好。有一个风险是当加密的交易不能及时上链，交易被解密。
优点： 对共识时间影响较小。矿工不需要花费额外的精力去处理交易解密本身。

门限密码系统 Threshshold Encryption

代表：ChainLink FSS
一种门限密码系统，该领域的基础门限密码学，是密码系统通过对信息进行加密并将其分发到容错计算机群集中来保护信息。该消息使用公钥，并且对应的私钥是共享参与方之间。使用阈值密码系统时，为了解密加密的消息或对消息进行签名，必须有多个参与方（超过某个阈值编号）进行解密或签名协议。

在Tendermint中，事务的执行在链上包含区块之后在块中进行。
每个验证器都有一份BLS门限解密密钥。任何2/3验证器可以使用这个密钥去解密一部分交易数据。
通过验证程序对Tendermint投票的时候必须包含对应部分解密数据的份额，交易的解密与共识最终状态的生成是同步进行的，即在没有最终确定块的情况下无法解密交易；如果交易不可解密，则无法最终确定块。

缺点： 在mempool中，为了支付解密手续费，有些数据无法加密。这里需要知道哪个帐户发送的交易，从而泄漏可以用作MEV边缘的信息。通过使用零知识证明使数据链上隐私，隐藏手续费的资金来源。必须使用泛拜占庭容错作为共识算法。

探索

同态加密

同态加密体系大致上被分为四类：部分同态、近似同态加密、有限级数全同态与完全同态。

• 加法同态：E(X)+E(Y) = E(X+Y)
• 乘法同态：E(X)E(Y) = E(XY)

满足上述两个公式的特性是全同态，满足期中之一就是半同态。

通俗来说，对原文的逻辑运算等于对密文的逻辑运算的解密。理论上所有的算术运算都可以归纳为加法和乘法。

零知识证明

定义：

• Succinct：简洁，证明的数据量比较小。
• Non-interactive：非交互，没有或者只有很少交互。
• ARguments：论证，讨论这些证明的一种形式主义，因为有一些花哨的密码学和非确定性并不能完全构成传统意义上的这些“形式证明”。
• Knowledge：知识，对于证明者来说在不知道证据（witness，比如一个哈希函数的输入或者一个确定Merkle-tree节点的路径）的情况下，构造出一组参数和证明是不可能的。
  零知识证明的目标是让验证者相信证明者拥有某个秘密(withness)，满足某种关系，而无需向验证者或其他任何人透露秘密本身。

零知识证明与dApp

在现有的基于零知识证明的区块链系统，一般有如下角色：证明者（Prover）和验证者（Verifier）
运用零知识证明系统我们可以轻松的用算术电路构建dApp（例如在：starkware、aleo上开发dApp），用户执行dApp，会生成Output和Proof。验证者不需要对交易本身进行re-execution（重放式验证），取而代之的是通过验证生成的Proof的正确性（Proof非常简洁，验证十分快速），即可保证Output的正确性（一定是按照dApp逻辑运行的）又可使验证复杂度与代码复杂度解藕。随后将Output提交到链上，逻辑代码处理链下化，链上只需要做状态数据通过Verifier检验后进行更改。极大的提升了链上处理数据的能力。

至此在理想情况下，我们可以使用零知识证明构建的dApp部署在服务器上。使用同态加密将私密数据进行加密，并在dApp中进行同态加密运算。将结果数据存储在区块链或链下的DHT中。
注：当不使用第三方Prover甚至不需要同态加密来做计算。Proof本身已经相当于隐私过了。

参考文献

https://www.zvstus.com/article/news/1/75d87ffffe84382c25d6d2d1c0f50000.html
https://www.youtube.com/watch?v=Hnw_tMGNx3A
https://docs.google.com/presentation/d/1tQEUpZjy_U9J-VQAx1Wf5W9oOX5rrCY3AwjAb7ZgA68/edit#slide=id.p
https://www.bilibili.com/video/BV1Ti4y1L7Ur
https://medium.com/starkware/presenting-veedo-e4bbff77c7ae
https://wanyvic.cn/posts/a5f2eb4
https://github.com/flashbots/pm
https://reading.supply/@whyrusleeping/a-vdf-explainer-5S6Ect
https://www.onlyalt.com/blog/mev-miner-extractable-value
https://www.youtube.com/watch?v=o08E4gx9TqA

全同态加密是什么

近几年对于个人隐私保护的话题越来越多，包括同态加密在内的一系列密码学应用技术也得到了很广泛的普及。在了解全同态加密（Fully Homomorphic Encryption/FHE）之前我们先了解下同态加密。

发展史

https://salt-security.com/nieuws/fully-homomorphic-encryption-de-geschiedenis/

同态加密

同态加密体系大致上被分为四类：部分同态、近似同态、有限级数全同态与完全同态。

部分同态加密

部分同态加密（Homomorphic encryption）也叫半同态加密，是一种加密形式，它允许人们对密文进行特定形式的代数运算得到仍然是加密的结果，将其解密所得到的结果与对明文进行同样的运算结果一样。
半同态加密模式：

• 加法同态：满足$E(X)E(Y)=E(X+Y)$。典型的例子为：椭圆曲线加密算法中，$E(x)=gx$（其中g为椭圆曲线的generator），则$E(x)E(y)=gxgy=g(x+y)=E(x+y)$，具有加法同态性。 以及Pedersen Commit也具有加法同态性。
• 乘法同态：满足$E(X)E(Y)=E(XY)$。典型的例子为：RSA加密算法中，$E(x)=x^e$（其中e为公钥），则$E(x)E(y)=x^ey^e=(xy)^e=E(xy)$，具有乘法同态性。

在加密计算中，加法同态可以完成任何加法运算。乘法同态亦然。

近似同态加密

如果我们又想让私密输入相乘，又想得到它们之间的线性组合的话，单纯的部分同态加密算法（RSA，ElGamal）是无法完成的。所以我们就需要来到下一阶段。

部分同态加密的下一阶段是近似同态加密，这一阶段距离我们想要实现的全同态更近了一步。如果我们有近似同态加密算法的话，那么我们就可以在密文上同时计算加法与乘法了。但是需要注意的是，正因为这一阶段是近似同态（Somewhat Homomorphic）的，所以可以做的加法和乘法次数非常有限，可以计算的函数也在一个有限的范围内。因为我们不能计算任意逻辑和深度的函数。

有限级数全同态加密

来到下一个阶段之后，我们距离全同态的目标更进一步了。

这一阶段被称之为有限级数全同态加密。在这一阶段的话，我们已经可以对密文进行任意的加法乘法组合了，没有任何对于次数的局限性。

但是之所以被称之为有限级数全同态的原因是，这个阶段的算法会引入一个新的复杂度上限$L$的概念，这一复杂度上限约束了函数$F$的复杂度。如果我们可以把$F$用二进制电路$C$来表示的话，那么$C$的深度和大小一定要在$L$的范围之内。

全同态加密

全同态加密的系统没有任何计算方法的限制，我们可以允许第三方对加密数据执行计算，并获得加密结果，他们可以将其交还给拥有原始数据解密密钥的任何人，而第三方无法自行解密数据或结果。

应用例子

假设您有一些电子邮件，您想通过第三方垃圾邮件过滤器来检查其中的垃圾邮件，又不希望第三方获取邮件中的内容。所有您可以使用全同态加密做以下方案：

这样第三方获取的是加密后的数据，他只需要在加密后的数据上做计算，将结果返回给您进行解密，即可得到计算后的原文结果。

对于区块链技术，同态加密也是很好的互补。使用同态加密技术，运行在区块链上的智能合约可以处理密文，而无法获知真实数据，极大的提高了隐私安全性。

目前全同态的加密方案主要包括如下三种类型：

• 基于理想格（ideal lattice）的方案：Gentry 和 Halevi 在 2011 年提出的基于理想格的方案可以实现 72 bit 的安全强度，对应的公钥大小约为 2.3 GB，同时刷新密文的处理时间需要几十分钟。
• 基于整数上近似 GCD 问题的方案：Dijk 等人在 2010 年提出的方案（及后续方案）采用了更简化的概念模型，可以降低公钥大小至几十 MB 量级。
• 基于带扰动学习（Learning With Errors，LWE）问题的方案：Brakerski 和 Vaikuntanathan 等在 2011 年左右提出了相关方案；Lopez-Alt A 等在 2012 年设计出多密钥全同态加密方案，接近实时多方安全计算的需求。

参考资料

https://yeasy.gitbook.io/blockchain_guide/05_crypto/homoencryption
https://vitalik.ca/general/2020/07/20/homomorphic.html

开篇提示

本文是基于V神Quadratic Arithmetic Programs: from Zero to Hero与网友分析基础之上总结而成。

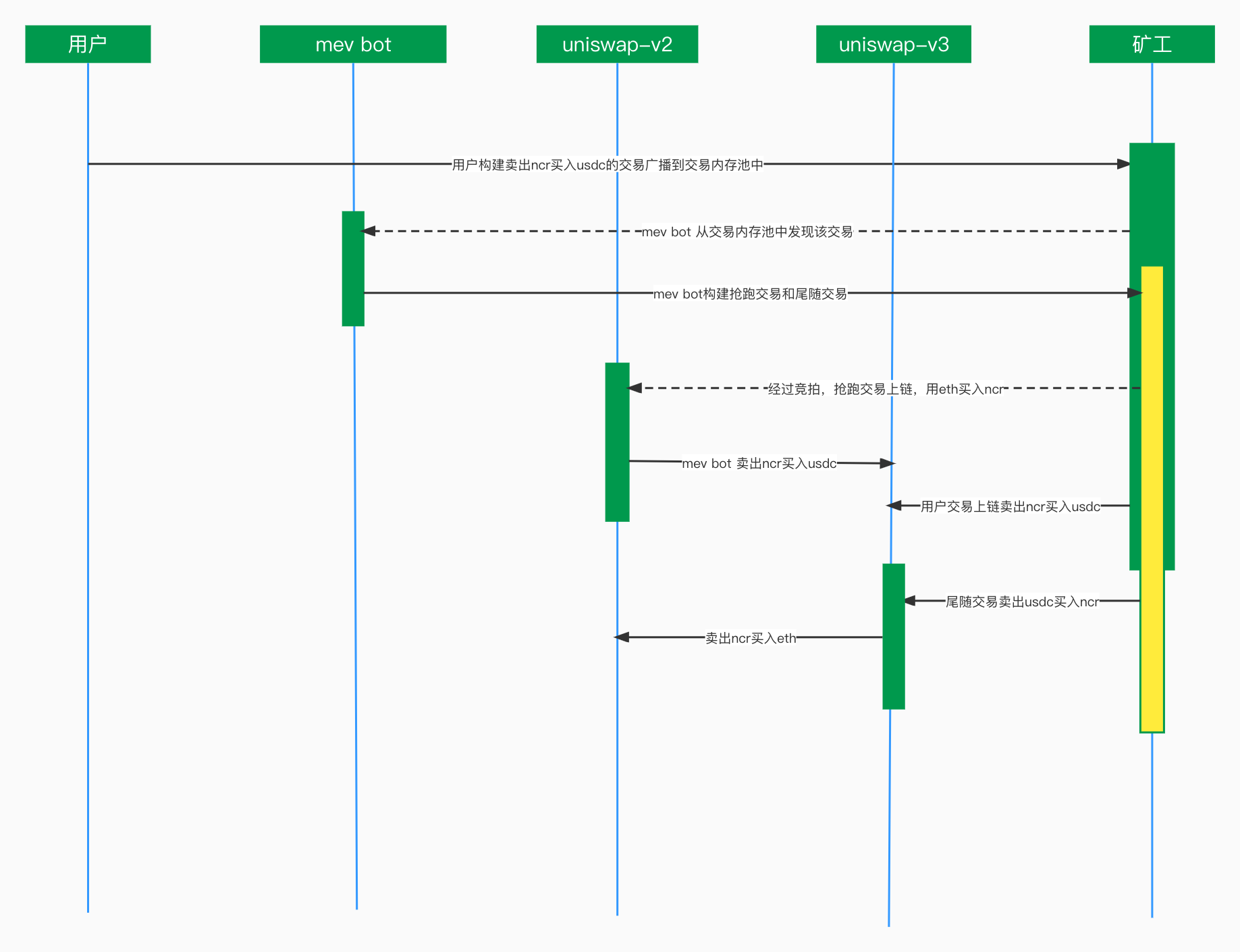
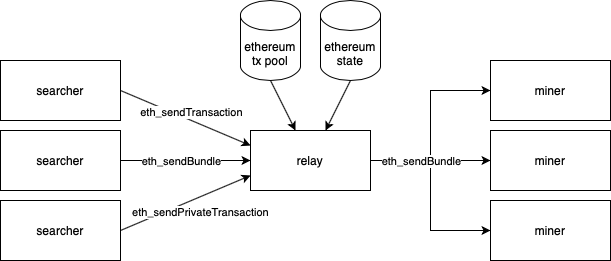
zkSNARK过程：

本篇只讲前半部分。

NP问题与NPC问题

• P问题：能在多项式时间内解决的问题。
• NP问题：能在多项式时间验证答案正确与否的问题。
• NP-hard问题：任意np问题都可以在多项式时间内归约为该问题。归约的意思是为了解决问题A，先将问题A归约为另一个问题B，解决问题B同时也间接解决了问题A。
• NPC问题：既是NP问题，也是NP-hard问题。

QAP 问题

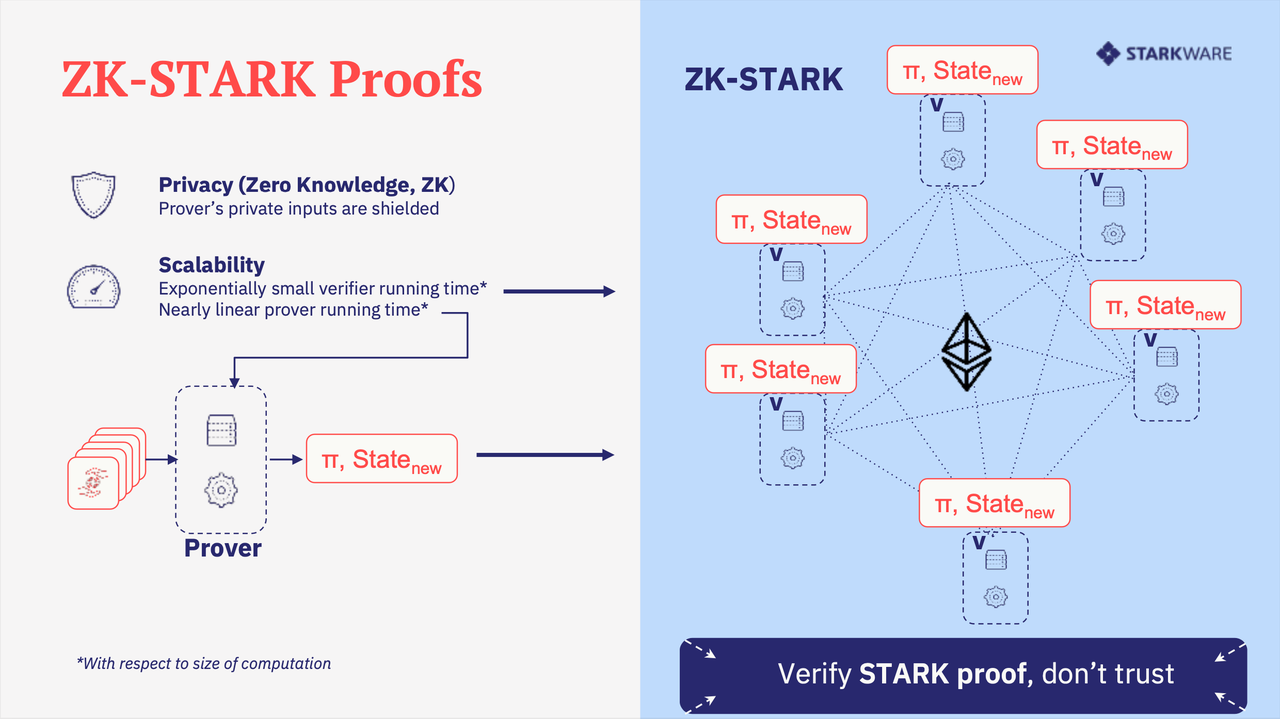
首先，zk-SNARK 不能直接用于解决任何计算问题，我们必须先把问题转换成正确的“形式”来处理，这种形式叫做 “quadratic arithmetic problem”(QAP)，在进行 QAP 转换的同时，如果你有代码的输入就可以创建一个对应的解（有时称之为 QAP 的 witness）。之后，还需要一个相当复杂的步骤来为 witness 创建实际的“零知识证明”，此外还有一个独立的过程来验证某人发送给你的证明。

我们来选择一个简单的例子来做说明：证明你知道一个立方方程的解：$x^3 + x + 5 = 35$ （提示：解是3，解用来构造 witness ）。这个例子既可以让你理解zkSNARK背后的技术原理，又不会产生出很大的 QAP。

def qeval(x):
    y = x**3
    return x + y + 5

我们这里所使用的特殊的程序语言支持基本算术运算 ($+,-,*,/$)，常量阶指数运算(如：可以计算 $x^7$ 但是不能计算 $x^y$ )和变量赋值，理论上可以在这个语言中做任意计算（只要计算步骤的次数是受限制的，此外，不允许循环）。注意，这个语言不支持模运算 ($\%$) 和比较运算 ($<, >, <=, >=$)，但是通过提供辅助输入可以扩展到支持这两种运算，此处我们不做展开。

扁平化

然后，我们把代码拍平(Flattening)转换为代数线路(algebraic circuit)：

拍平后的代码一次只能做下面的一种简单运算，x=y（x可以是数字或变量）。x=y op z（其中op可以是$+,-,*,/$等运算）

$sym\_1 = x * x$
$y = sym\_1 * x$
$sym\_2 = y + x$
~$out = sym\_2 + 5$

在上面的过程中，我们引入了一些中间变量，但是整体跟我们原来的的代码是等价的。

通往 R1CS 的大门

接下来，我们需要把拍平的代码写成一个叫作R1CS（rank-1 constraint system）的约束系统。

R1CS： 可将其理解为一个方程组。

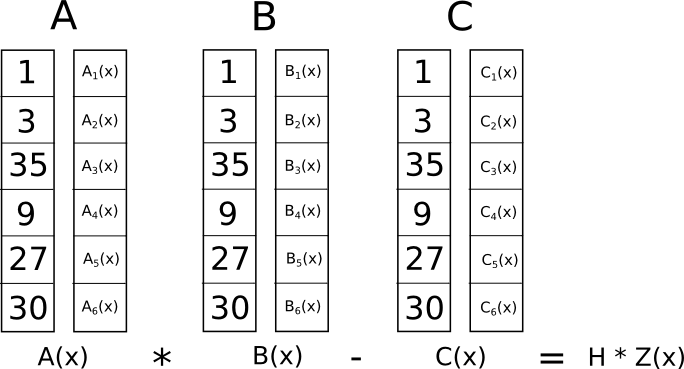
Prover需要向Verifier证明其知道满足该方程组所有方程式的解，证明过程可转化为Prover知道3组向量$(\vec{a},\vec{b},\vec{c})$以及1组对应于R1CS解的向量$\vec{s}$（np问题转化为np完全问题），使得$<\vec{s},\vec{a}>*<\vec{s},\vec{b}>-<\vec{s},\vec{c}>=0$成立。

其中$<\vec{s},\vec{a}>=\sum_{i=1}^{n}$。

拍平后的方程组：

$sym\_1 = x * x$
$y = sym\_1 * x$
$sym\_2 = y + x$
~$out = sym\_2 + 5$

由方程组可知，其中涉及6个变量和4个逻辑门。

左侧组成了变量组，在此基础上加上$1$和$x$，组成了6维向量$\vec{s}=[ \text{\textasciitilde}one,x,\text{\textasciitilde}out,sym\_1,y,sym\_2 ]$

其中：

• $\text{\textasciitilde}one$：虚拟变量
• $x$：输入变量
• $\text{\textasciitilde}out$：输出变量

Prover知道满足上述方程式组的解（$x=3$），则$\vec{s}=[ \text{\textasciitilde}one,x,\text{\textasciitilde}out,sym\_1,y,sym\_2 ] = [1,3,35,9,27,30]$。

计算

第一门逻辑电路

$y=sym_1*x$，满足$<\vec{s},\vec{a}>*<\vec{s},\vec{b}>-<\vec{s},\vec{c}>=0$成立的$(\vec{a},\vec{b},\vec{c})$为：

$\vec{a} = [0,1,0,0,0,0]$
$\vec{b} = [0,1,0,0,0,0]$
$\vec{c} = [0,0,0,1,0,0]$

$<\vec{s},\vec{a}>*<\vec{s},\vec{b}>-<\vec{s},\vec{c}>= 3*3-9=0$

第二门逻辑电路

$y=sym\_1*x$，满足$<\vec{s},\vec{a}>*<\vec{s},\vec{b}>-<\vec{s},\vec{c}>=0$成立的$(\vec{a},\vec{b},\vec{c})$为：

$\vec{a} = [0,0,0,1,0,0]$
$\vec{b} = [0,1,0,0,0,0]$
$\vec{c} = [0,0,0,0,1,0]$

第三门逻辑电路

$sym\_2=y+x$，满足$<\vec{s},\vec{a}>*<\vec{s},\vec{b}>-<\vec{s},\vec{c}>=0$成立的$(\vec{a},\vec{b},\vec{c})$为：

因为是加法所以这里做法有些不同（实际转化为$sym\_2=(y+x)*1$）：
$\vec{a} = [0,1,0,0,1,0]$
$\vec{b} = [1,0,0,0,0,0]$
$\vec{c} = [0,0,0,0,0,1]$

$<\vec{s},\vec{a}>*<\vec{s},\vec{b}>-<\vec{s},\vec{c}>= (3+27)*1-30=0$

第四门逻辑电路

$\text{\textasciitilde}out=sym\_2+5$，满足$<\vec{s},\vec{a}>*<\vec{s},\vec{b}>-<\vec{s},\vec{c}>=0$成立的$(\vec{a},\vec{b},\vec{c})$为：

$\vec{a} = [5,0,0,0,0,1]$
$\vec{b} = [1,0,0,0,0,0]$
$\vec{c} = [0,0,1,0,0,0]$

$<\vec{s},\vec{a}>*<\vec{s},\vec{b}>-<\vec{s},\vec{c}>= (5+30)*1-35=0$

最后得到完整的R1CS：

A:
$[0, 1, 0, 0, 0, 0]$
$[0, 0, 0, 1, 0, 0]$
$[0, 1, 0, 0, 1, 0]$
$[5, 0, 0, 0, 0, 1]$

B:
$[0, 1, 0, 0, 0, 0]$
$[0, 1, 0, 0, 0, 0]$
$[1, 0, 0, 0, 0, 0]$
$[1, 0, 0, 0, 0, 0]$

C:
$[0, 0, 0, 1, 0, 0]$
$[0, 0, 0, 0, 1, 0]$
$[0, 0, 0, 0, 0, 1]$
$[0, 0, 1, 0, 0, 0]$

R1CS to QAP

下一步是将这个 R1CS 转换成 QAP 形式。它实现了完全相同的逻辑，只是使用了多项式而不是点积。

通过使用拉格朗日插值或快速傅里叶逆变换来将4组长度为6的三个向量转换为3组6个3次多项式。

具体作法：
从每个a向量中取出一个值，用拉格朗日插值来构造一个多项式(在 i 处的多项式得到 i 的第一个值)

从第一列得到$(1,0),(2,0),(3,0),(4,5)$使用这4个点用拉格朗日插值构造多项式，以此类推。

最后得到多项式

A polynomials
$[-5.0, 9.166, -5.0, 0.833]$
$[8.0, -11.333, 5.0, -0.666]$
$[0.0, 0.0, 0.0, 0.0]$
$[-6.0, 9.5, -4.0, 0.5]$
$[4.0, -7.0, 3.5, -0.5]$
$[-1.0, 1.833, -1.0, 0.166]$

B polynomials
$[3.0, -5.166, 2.5, -0.333]$
$[-2.0, 5.166, -2.5, 0.333]$
$[0.0, 0.0, 0.0, 0.0]$
$[0.0, 0.0, 0.0, 0.0]$
$[0.0, 0.0, 0.0, 0.0]$
$[0.0, 0.0, 0.0, 0.0]$

C polynomials
$[0.0, 0.0, 0.0, 0.0]$
$[0.0, 0.0, 0.0, 0.0]$
$[-1.0, 1.833, -1.0, 0.166]$
$[4.0, -4.333, 1.5, -0.166]$
$[-6.0, 9.5, -4.0, 0.5]$
$[4.0, -7.0, 3.5, -0.5]$

系数按升序排列，所以上面的第一个多项式实际上是$0.833x^3-5x^2 + 9.166x-5$。这组多项式(加上我稍后解释的 z 多项式)构成了这个特定 QAP 实例的参数。

检查 QAP

我们可以将x带入多项式，例如$x=1$

A results at x=1
$0\\ 1\\ 0\\ 0\\ 0\\ 0\\$

B results at x=1
$0\\ 1\\ 0\\ 0\\ 0\\ 0\\$

C results at x=1
$0\\ 0\\ 0\\ 1\\ 0\\ 0\\$

这里有的，和我们上面创建的第一个逻辑门的，三个向量的集合完全一样。

与其单一检查R1CS的约束不如对多项式进行点积同时来检查所有的约束。

例如当$x=1$时：
$A(1)=1*(-5)+3*8+35*0+9*(-6)+27*4+30*(-1)=43$
$A(2)=1*9.166+3*(-11.333)+35*0+9*9.5+27*(-7)+30*1.833=-73.333$
…

得出：
$A \cdot s = [43.0, -73.333, 38.5, -5.166]$
$B \cdot s = [-3.0, 10.333, -5.0, 0.666]$
$C \cdot s = [-41.0, 71.666, -24.5, 2.833]$

$A \cdot s*B \cdot s -C\cdot s$$=(-5.166x^3+38.5x^2-73.333x+43)*(0.666x^3-5x^2+10.333x-3)-(2.833*x^3-24.5*x^2+71.666x-41)=-3.444x^6+51.5x^5-294.777x^4+805.833x^3-1063.777x^2+592.666x-88$

$t=[-88.0, 592.666, -1063.777,\allowbreak 805.833, -294.777, 51.5, -3.444]$

Z定义为$(x-1)(x-2)(x-3)...$在对应于逻辑门的所有点处为零的最简单多项式。代数的一个基本事实是，任何在所有这些点上都等于 0 的多项式必须是这个最小多项式的倍数。即Z应该为t的因式。

计算：

$Z =(x-1)(x-2)(x-3)(x-4)=[24,-50,35,-10,1]$

$H = t/Z = [-3.666,17.055,-3.444]$ (wolframalpha 计算有误差)

精确值：$H = t/z = -\frac{31}{9}x^2+\frac{307}{18}x-\frac{66}{18}$

即：t可被Z整除。即Z为t的因式。

如果我们试图伪造 R1CS 解决方案中的任何变量。则t不会是Z的倍数。

参考资料

https://james-christopher-ray.medium.com/here-are-the-calculations-for-the-product-of-a-b-and-c-with-s-ae6a3f94647a
https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649

多项式

零知识采用多项式充当证明的媒介。

其中涉及到代数基本定理：

• 任何复系数一元n次多项式，方程在复数域上至少有一根(n≥1)，由此推出，n次复系数多项式方程在复数域内有且只有n个根。

进而可推出，当两个次数相同的一元n次多项式有且只有n个交点。

示例

假设验证者手中有一个一元n次多项式。

证明者声称他知道验证者的多项式。

他们可以使用以下的方式进行交互：

• 验证者选出一个随机的值$x$，并求出多项式结果。
• 验证者把$x$给证明者，要求证明者对$x$进行求值。
• 证明者将结果给验证者。
• 验证者检验证明者给的值是否与自己计算的一致。如果一致那么这个语句将会有很大程度是真的。

例如，如果我们考虑$x$的整数范围从1到$10^{77}$，不同多项式的非交点最少为是$10^{77}-d$ ($d$：次数)，因此$x$意外“命中”任何$d$的交点的概率等于(微不足道的) :

$$\frac{d}{10^{77}}$$

假设$d$足够小于范围的上限，几乎是100%

参考资料

https://medium.com/@imolfar/why-and-how-zk-snark-works-1-introduction-the-medium-of-a-proof-d946e931160

介绍

零知识证明的目标是让验证者相信证明者拥有某个秘密(withness)，满足某种关系，而无需向验证者或其他任何人透露秘密本身。

我们可以更具体地认为这是一个程序，表示为C，接受两个输入：C(x, w)。输入x是公共输入，w是秘密见证输入(区块链内一般指交易本身)。该程序的输出是布尔值，即true或false。随后的目标是给出了具体的公共投入x，证明了证明方知道秘密输入w这样C(x,w) == true。

示例程序

假设Bob知道一个散列值H，并且他希望有一个证明，证明Alice知道s的散列的值是H。通常 Alice会通过把s给Bob来证明这一点，之后Bob会重新计算哈希并检查它是否等于H。

但是，假设Alice不想把s透露给Bob，而只是想证明她知道该值。她可以为此使用zk-SNARK。

function C(x, w) { 
  return ( sha256(w) == x ); 
}

其中w就代表了秘密s，x代表公开值H，C(x, w)就代表了证明(proofs)。Bob只需要验证C(x, w)是否为true即可相信Alice，而无须知道s本身。

zk-SNARK 的定义

一个zk-SNARK由三个算法组成，G, P, V定义如下：

密钥生成器G接受一个秘密参数lambda和一个程序电路C，并生成两个公开可用的密钥，一个证明密钥pk和一个验证密钥vk。这些密钥是公共参数，只需要为给定程序C生成一次。

证明者将P证明密钥pk、公共输入x和隐私见证作输入w。该算法生成证明prf = P(pk, x, w)。

验证者V计算证明prf，如果正确则V(vk, x, prf)返回true，否则返回false。因此，如果证明者知道w，则此函数C(x,w) == true

请注意此处生成器中使用的秘密参数lambda。这个参数有时会让在实际应用中使zk-SNARK变得很棘手。这样做的原因是任何知道这个参数的人都可以生成假证明。具体来说，给定任何程序C和公共输入x，知道lambda的人可以生成一个证明fake_prf，以便在不知道秘密w的情况下使V(vk, x, fake_prf)等于true。

因此，实际运行生成器需要一个非常安全的过程，以确保没有人知道并将参数保存在任何地方。这就是Zcash团队为了生成证明密钥和验证密钥而进行了极其精心的仪式的原因，确保lambda在此过程中被销毁。

给我们的示例使用zk-SNARK

Alice和Bob在实践中如何使用zk-SNARK来证明Alice知道上面例子中的秘密值？

首先，如上所述，我们将使用一个由以下函数定义的程序:

function C(x, w) { 
  return ( sha256(w) == x ); 
}

Bob的第一步是运行生成器g，以创建验证密钥pk和验证密钥vk。首先随机生成 lambda并使用它作为输入:

(pk, vk) = G(C, lambda)

正如上面所讨论的，必须小心处理lambda参数，因为如果Alice知道lambda的值，她将能够创建伪证明。Bob将与Alice分享pk和vk。

Alice现在将扮演证明者的角色。她需要证明她知道散列到已知hash H的值s。她运行证明算法 P，输入pk,H和s来生成证明prf:

prf = P(pk, H, s)

接下来，Alice把证明文件交给Bob，Bob运行验证函数v(vk,H,prf) ，在这种情况下返回 true，因为Alice完全知道这个秘密。Bob可以确信Alice知道这个秘密，但Alice不需要向Bob透露这个秘密。

可重用的证明和验证密钥

在我们上面的示例中，如果Bob想向Alice证明他知道一个s'，就不能使用上面的过程了。这是因为Alice不知道Bob有没有保存lambda参数。如果保存了，Bob有能力伪造证明。

如果一个程序对许多人有用(比如 Zcash 的例子) ，一个独立于Alice和Bob的可信任的第三方可以运行生成器并创建证明密钥pk和验证密钥vk，这样就没有人知道lambda了。

任何信任这个第三方的人都可以在未来的交互中使用这些密钥。

Ethereum 中的 zk-snark

开发者已经开始将zk-snark集成到Ethereum中。这看起来像什么？具体而言，验证算法（verify）的构建模块以预编译合同的形式添加到Ethereum。用法如下: 生成器链下运行，生成验证密钥和验证密钥。然后，任何证明者都可以使用proving key来创建证明，也是链下运行的。通用验证算法可以在一个智能合约中运行，使用pk、vk和公共输入作为输入参数。验证算法的结果可以用于触发其他链上活动。

这里有一个简单的例子来说明zk-snark如何帮助保护Ethereum上的隐私。假设我们有一个简单Token合约。一般来说，常规的合同（ERC20）是从地址到余额的映射：

mapping (address => uint256) balances;

我们将用余额的散列替换余额，bytes32代替uint256。

mapping (address => bytes32) balanceHashes;

我们不会隐藏交易的发送者或接收者，但是我们可以隐藏余额和发送量。这种财产有时被称为机密交易。

两个zk-snark用于将令牌从一个帐户发送到另一个帐户，一个由发送者创建，一个由接收者创建。（发送者生成发送的proof，接收者生成接收的proof）

通常在一个Token合约中，如果一个交易金额是有效的，我们需要验证以下内容:

balances[fromAddress] >= value

因此，我们也需要在zk-snark证明更新后的哈希值与更新后的余额相匹配。

其主要思想是，发送者将使用他们的startBalance和交易value作为隐私输入，将startBalance、afterBalance和value的哈希作为公共输入。类似地，接收者将startBalance和value作为秘密输入，将startBalance、afterBalance和value的哈希作为公共输入。

下面是我们将用于发送方zk-SNARK的程序，其中与前面一样，x表示公共输入，w表示私有输入。

function senderFunction(x, w) {
  return (
    w.senderBalanceBefore > w.value &&
    sha256(w.value) == x.hashValue &&
    sha256(w.senderBalanceBefore) == x.hashSenderBalanceBefore &&
    sha256(w.senderBalanceBefore - w.value) == x.hashSenderBalanceAfter
  )
}

接收方使用的程序如下:

function receiverFunction(x, w) {
  return (
    sha256(w.value) == x.hashValue &&
    sha256(w.receiverBalanceBefore) == x.hashReceiverBalanceBefore &&
    sha256(w.receiverBalanceBefore + w.value) == x.hashReceiverBalanceAfter
  )
}

程序检查发送余额是否大于正在发送的值，并检查所有散列是否匹配。一组可信的人员将为我们的 zk-snark生成证明和验证密钥，我们称之为confTxSenderPk、confTxSenderVk、conftxreceivpk和confTxReceiverPk。

使用zk-snark的Token合约看起来像这样:

function transfer(address _to, bytes32 hashValue, bytes32 hashSenderBalanceAfter, bytes32 hashReceiverBalanceAfter, bytes zkProofSender, bytes zkProofReceiver) {
  bytes32 hashSenderBalanceBefore = balanceHashes[msg.sender];
  bytes32 hashReceiverBalanceBefore = balanceHashes[_to];
  
  bool senderProofIsCorrect = zksnarkverify(confTxSenderVk, [hashSenderBalanceBefore, hashSenderBalanceAfter, hashValue], zkProofSender);

bool receiverProofIsCorrect = zksnarkverify(confTxReceiverVk, [hashReceiverBalanceBefore, hashReceiverBalanceAfter, hashValue], zkProofReceiver);

  if(senderProofIsCorrect && receiverProofIsCorrect) {
    balanceHashes[msg.sender] = hashSenderBalanceAfter;
    balanceHashes[_to] = hashReceiverBalanceAfter;
  }
}

因此，区块链上唯一的更新是balance的hash，而不是balance本身。然而，我们可以知道所有的balance是正确的更新，因为我们可以检查自己的证明已经验证。

上述机密事务方案主要是给出了一个如何在 Ethereum 上使用 zk-snark 的实例。为了在此基础上创建一个健壮的机密事务方案，我们需要解决一些问题:

• 用户将需要跟踪他们的余额客户端，如果您失去了余额，这些令牌是不可恢复的。也许可以使用从签名密钥派生的密钥对余额进行链式加密存储。注： 要用户记录自己的w，或存储在链上。
• 余额需要使用32字节的数据和编码熵的平衡的一部分，以防止能够扭转哈希算出余额。注： 对balanceHash加salt避免字典攻击。
• 需要处理发送到未使用地址的边缘情况。
• 为了发送，发送者需要与接收者互动。一个可能有一个系统，其中发送者使用他们的证据来启动交易，和接收者可以看到在块环链上，他们有一个“未决的传入交易”，并可以完成它。注： 必须要有个链下的撮合系统收集发送者和接收者的proof。

参考

https://media.consensys.net/introduction-to-zksnarks-with-examples-3283b554fc3b

介绍

本次以拆解DefiKingdoms项目的NFT方面为主。

关于审计

目前在官方文档中找到关于defi的审计，关于gamefi的审计未找到。

关于源码

目前找到关于defi源码，NFT源码未公开、未验证。

ERC20

ERC721

NFT：one1ta6nmn0ekxke427px3npf505w3hadnjuhlh7vv

玩法

Marketplace

交易市场可以交易Token、流动性和买卖部分游戏物品。

Druid

流动性相关，DEX常规玩法（uniswap）：

1. 创建流动性
2. 添加流动性

合约地址：one1yjkky5pdr3jje3mggzq3d8gy394vyresl69pgt

Trader

DEX的swap交易功能相关

Vendor

使用DFKGOLD买卖专业任务获得的部分物品。

合约地址：one1u5al0rutnxmdx4he8aq6lwv4z95vegkxj3wh82
合约交互：

• buyItem 买物品
• 096c5e1a 卖物品

Gardens

DEX的存入lp挖JEWEL

1. 每个Epoch是302400个区块。每个Epoch执行相对应的系数减产。
2. 并且获得的JEWEL按Epoch给的系数部分锁定。

详细参数

Bank

存JEWEL得到xJEWEL类似xsushi。收入来源dex手续费、流动性撤出手续费和游戏手续费。

合约地址：one1488gx5rasuk9uynnuaz6hn76sjw65e206pmljg

合约交互：

• enter 存入
• leave 取出

Tevern

查看、买卖和出租英雄。本质上是个NFTMarketPlace。购买时抽手续费给dev、bank。

NFTMarketPlace：

• one1zwn9h8uq883vqv4uqgshrhq9kvxr72yjjjz9la

合约交互：

• createAction：设置卖单
• cancelAction：撤销卖单
• bid：购买英雄

Portal

• 召唤需要两个英雄和消耗DFKTEARS和JEWEL合成召唤水晶，然后调用Open开启水晶得到新的召唤英雄。
• 召唤次数是有固定的限制。并且召唤消耗的DFKTEARS随着英雄等级而提高。
• 召唤英雄基因会继承和随机突变上代。

召唤相关合约：
one17nf6ugpvntj3daltrk66luvm76v6tc648l0sva

合约交互：

• 租用召唤：c2b40631
• 合成召唤水晶：summonCrystal
• 打开水晶：open

Professions

任务系统，不同的职业通过任务获得不同的产出：

• 消耗耐力，有几率得到产出。
• 参与职业任务获得JEWEL和游戏内资源，以及提升职业技能和经验。
• 当前只有fisher和forager职业开放，其他职业暂未推出。
• 英雄的基因会影响获得奖励的几率和减少耐力消耗。
• 不同的职业获取的游戏物品不一。
• 游戏物品可以去Vendor交易，也可以用于炼金合成。

Fishing：

• 消耗耐力得到经验和钓鱼的技能提升。有几率得到与钓鱼相关的物品，相关物品可以在Vendor售卖或在Alchemist合成药水。

Foraging：

• 消耗耐力得到经验和觅食的技能提升。有几率得到与植物相关的物品，相关物品可以在Vendor售卖或在Alchemist合成药水。

one12yqt6vdcygm3zz9q7c7uldjefwv3n6h5trltq4

合约交互：

• startQuest 开始任务
• completeQuest 完成任务获得奖励

Docks

跳转到跨链桥功能。

Meditation Circle

英雄升级：

当在任务系统中累积足够的经验即可在此升级，需要消耗JEWEL和专业符文(专业任务中产出)。也可以消耗水晶提升某属性的成功率。

合约地址：one1qk2ds6efyvrk5gckat4yu89zsmd2zskpwyytuq

合约交互：

• startMeditation 开始升级
• completeMeditation 完成升级

Alchemist

炼金术师使用多个专业物品合成药水。

总结

DefiKingdoms与传统的NFT开盲盒、合成、消耗、抽奖的机制基本无差。相较于同类型游戏玩法稍复杂、可玩性较强。

游戏本质是通过一系列的游戏玩法，设置产出和消耗与门槛使参与游戏的部分玩家获得获利，从而达到财富再分配。

Star Atlas

官网：https://staratlas.com/

Star Atlas是一个基于2620年的虚拟元宇宙游戏。基于虚幻5开发的3A MMORPG游戏（链游版的EVE）。故事背景设定在 2620 年，在官方设定中，宇宙分为了三大派系：由人类统治的 MUD 领地；外星种族联盟的 ONI 区域；知觉机器人控制的 Ustur 星区。三大派系为资源、领土和统治权进行着持续的战争。玩家可自由加入其中一方，为自己的派系贡献力量。而玩家的行为则将直接影响这场星际冲突的结果，通过在游戏中做出贡献，玩家可获得代币奖励。

特点：

• 资产链上化（NFT）：舰船、船员、宠物、组件、土地、建筑物、服装等等
• 双代币经济体系

通证

游戏中也将实行双通证，ATLAS和POLIS。

ATLAS： ATLAS将作为游戏内的主要交易媒介，用于购买游戏内的土地、装备、组件等等，总量360亿。

POLIS： 项目的治理通证，将用于参与决策游戏内的一些玩法和机制，总量3.6亿。

进展

• 第一阶段：OpenSea资产售卖
• 第二阶段：网页迷你小游戏
• 第三阶段：船坞组件售卖
• 第四阶段：最终预售公测
• 第五阶段：持续售卖

当前进展：阶段二，玩家可以在marketplace上自由买卖NFT。关于3A游戏本身暂未看到任何进度。按3A大作开发惯例，一般需要5-10年不等。

github

当前github主要开源一个与token解锁相关智能合约的仓库 token-vesting

关于dex-Serum

solana上的所有DEX都基于Serum，也就是说只要你知道了某一交易对的Market ID，你可以在任何前端进入交易。用SA举例就是你要买飞船，不用在官网买，直接在支持Serum的任意前端导入market ID，就可以进行交易，查看订单。

Fancy Birds

官网：https://www.fancybirds.io/

merit-circle投资。玩法类似于2013年大火的flappy bird。一共发行8888只创世鸟。拥有繁殖、遗传基因玩法，罕见的基因可以提升打金收入。玩法本质上类似于Axie Infinity。

当前进度

• token已发行：FNC
• 2021年12月15日上线质押挖矿(Defi 挖矿玩法)
• 预计2022 Q1上线创世鸟的铸造和marketplace
• 预计2022 Q2上线游戏主体

github

审计报告中找到的地址，打不开。
似乎未开源：https://github.com/Fancy-Birds/
审计报告包含Token和staking相关的合约代码审计

defi 玩法

常规defi玩法，质押FNC或LP挖矿。
https://staking.fancybirds.io/

通证

Fancy Token($FNC)

Staked Fancy Games LP(锁仓SLP挖矿合约)

sushi FNC-WETH lp (SLP)

游戏模式

• PVP、PVE打金。（flappy bird有类似的辅助软件）
• 交易、繁殖、锦标赛（玩法类似于Axie Infinity）。
• 后续sFNC用于游戏经济中的繁殖、赌注和其他游戏内活动。

技术手段猜测

由于代码未开源，现根据游戏玩法对技术的猜测

1. 使用Immutable X发行、交易、跨链NFT，和FNC（DAO）。
2. 基于starknet Cairo开发繁殖、PVP、PVE奖金系统。

DefiKingdoms

https://defikingdoms.com/
DeFi Kingdoms是基于Harmony Protocol区块链开发的一款play2earn游戏。

DeFi Kingdoms旨在将DeFi元素包装成一个成为一个完整的功能生态系统。
本质上还是个DEX+NFT。

通证

JEWEL：0x72cb10c6bfa5624dd07ef608027e366bd690048f

xJEWEL：0xa9ce83507d872c5e1273e745abcfda849daa654f

github

部分合约：https://github.com/DefiKingdoms/contracts/

• AidropClaim.sol： 空投相关的合约很简单，merkeproof都没有用到
• Bank.sol：质押JEWEL挖矿，使用的xsushi代码base
• Banker.sol：一个将合约内部的lp解除流动性并将token转换成JEWEL存入Bank合约中。lp来源swap的feeTo。
• MasterGardener.sol：流动性矿池类似于masterchef
• UniswapV2Factory.sol: uniswap的代码base，feeTo设置为Banker
• UniswapV2Router02.sol

NFT

玩家可以通过购买、合成、售卖等方式玩NFT获利。NFT可以影响defi的收益。

• Gen0：2090只创世英雄
• 稀有度：紫、橙、蓝、绿、白
• 英雄职业和专业影响defi的收益
• 特定的职业+特定的专业以及稀有度可以最大化收益产出，玩家主要就是合成此类卡片售卖或挖矿。

专业功能未开放

• mining：可以提前解锁JEWEL和黄金（黄金Token未上线）
• Gardening：增加流动性挖矿利率
• Fishing：可以获得宝物
• Foraging：可以炼制素材

职业

职业分基础职业、进阶职业、精英职业。最上级职业。

两个职业可以合成上阶职业（有合成率）。

合成次数从职业低到高，有不同的限制，越往上合成次数越少。